El test exacto de Fisher
Es una prueba de significación estadística utilizada en el análisis de tablas de contingencia. Aunque en la práctica se emplea cuando los tamaños de muestra son pequeños, también es válido para todos los tamaños de muestra.
La prueba es útil para los datos categóricos que resultan de clasificar los objetos en dos formas diferentes, se utiliza para examinar la significación de la asociación entre los dos tipos de clasificación
La mayoría de los usos de la prueba de Fisher implican una tabla de 2×2 de contingencia. El valor de p de la prueba se calcula como si los márgenes de la tabla fueran fijos
La catadora de té
La catadora de té (lady tasting tea) es un experimento aleatorizado que Ronald Fisher desarrolló y presentó en su libro The Design of Experiments (1935). Con este experimento, Fisher introdujo el concepto de la hipótesis nula.
El ejemplo se basó vagamente en un evento real ocurrido en la vida de Fisher, la mujer fue Muriel Bristol y la prueba usada fue el test exacto de Fisher.
El experimento
La mujer dijo que podía distinguir, en una taza cualquiera de té con leche, si se había vertido primero la leche o primero el té, una distinción importante en la cultura de inglesa.
Fisher propuso darle ocho tazas, cuatro de cada variedad, en un orden aleatorio. Luego podría preguntarse cuál fue la probabilidad de que ella descubriera correctamente cuáles tazas habían recibido primero la leche o primero el té, únicamente de manera aleatoria.
- En el experimento, se le dieron a la mujer 8 tazas ordenadas aleatoriamente – en cuatro de ellas, la leche se había agregado primero; en las otras cuatro el té. Ella tenía que indicar cuáles 4 tazas pertenecían a cada grupo.
- Se le dio la ventaja de juzgar las tazas por comparación.
- Se le informó a la mujer todo lo relativo al experimento.
- La hipótesis nula suponía que la mujer no tenía la capacidad de distinguir las tazas.
- Según la manera en la que Fisher abordó el problema, no existe una hipótesis alternativa.
- El test estadístico fue un simple recuento del número de éxitos de seleccionar 4 tazas correctas.
- La distribución de la hipótesis nula se calculó a través del número de permutaciones.
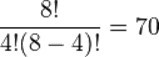
Calculando la combinaciones con n = 8 tazas totales y k = 4 tazas seleccionadas, existen 70 combinaciones posibles.
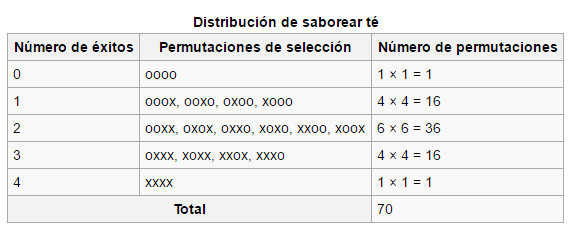
- La región crítica fue el caso único de cuatro éxitos de cuatro posibles, a partir de criterios convencionales de probabilidad (< 5%; 1 sobre 70 ≈ 1.4%).
Si y solo si la mujer lograra clasificar correctamente las ocho tazas, Fisher rechazaría la hipótesis nula – y reconocía, por consiguiente, la habilidad de la mujer a un nivel de significancia de 1.4% (pero sin cuantificar su habilidad).

